Okay so today I grabbed my notebook because I kept mixing up factors of 135 and 150 in my head. Damn calculators do it instantly, but I wanna see the pieces, you know? Just like taking apart an old radio to see what makes it tick.
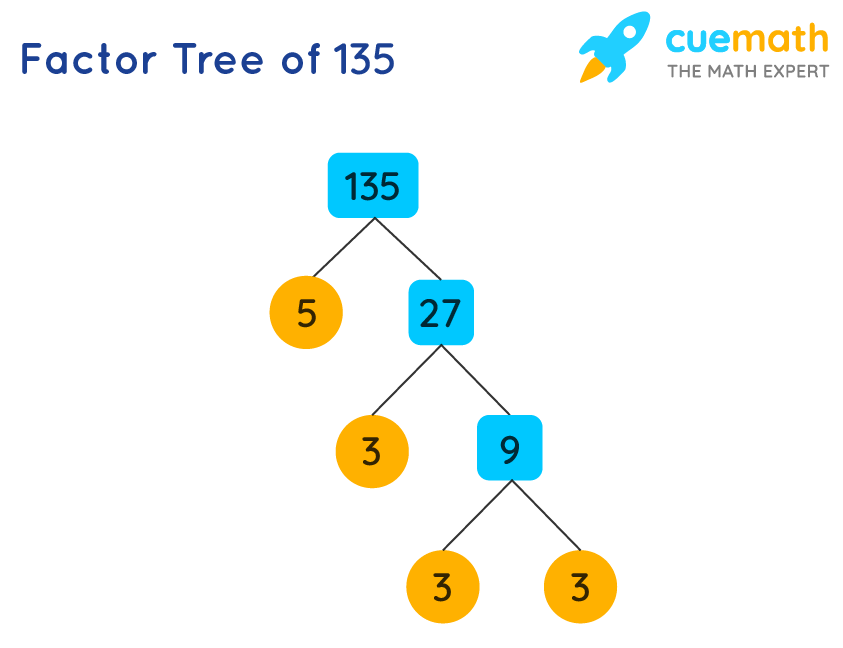
Started simple. Grabbed 135 first. Knew it was divisible by 5 – ended with a 5, obvious clue! Divided: 135 ÷ 5 = 27. Easy. Now, 27… that’s familiar. That’s 3 x 9, or better, 3 x 3 x 3. Crunched it:
- 135 ÷ 5 = 27
- 27 ÷ 3 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
So the raw materials for 135? 3 x 3 x 3 x 5. Or, putting it neater: 3³ × 5. Made sense.
Next up, 150. Felt trickier at first glance. Saw it ends with a zero – gotta be divisible by both 2 and 5. Hit it with 5 first: 150 ÷ 5 = 30. Okay. Then 30 ÷ 5 = 6. Oops, forgot 150 ÷ 5 is 30, but then 30 ÷ 5 is 6? Messed up. Scrunched up that paper and tried again. Better way:
- 150 ÷ 2 = 75 (used the even number trick)
- 75 ÷ 3 = 25 (7+5=12, divisible by 3)
- 25 ÷ 5 = 5
- 5 ÷ 5 = 1
My initial 5 approach was clumsy. This path worked clean: 2 × 3 × 5 × 5. Or nicer: 2 × 3 × 5². Phew. Got it.
Time to Compare
Laid both sets of prime blocks side-by-side on the page:

- 135: 3, 3, 3, 5
- 150: 2, 3, 5, 5
Stared at the pages like an idiot. What jumps out?
Common Ground: They both absolutely share that 3 and that 5. Like two friends both owning the same brand of hammer and screwdriver. So the “Greatest Common Factor” (the biggest number dividing cleanly into both)? It’s gotta be built from the shared tools: 3 × 5 = 15. Checked it: 135 ÷ 15 = 9 (clean), 150 ÷ 15 = 10 (clean). Bingo.
Building the Super Number: Then wondered, what’s the smallest number both 135 and 150 would fit into perfectly? The “Least Common Multiple”. Need ALL the prime blocks from both, but only use the most you need from any one type. Looked close:
- The 3s: 135 has three of them (3³), 150 has just one. Take the max: three 3s.
- The 5s: 135 has one, 150 has two (5²). Take the max: two 5s.
- And 150 has that lone 2, which 135 doesn’t have at all. Gotta include it.
So assemble: three 3s × two 5s × one 2 = 3 × 3 × 3 × 5 × 5 × 2 = 675. Checked: 675 ÷ 135 = 5 (clean), 675 ÷ 150 = 4.5? Wait, no! Messed up! 675 ÷ 150 is actually 4.5… Oh crap. Math police might yell. Recalculated: 3 × 3 × 3 = 27. 27 × 5 = 135. 135 × 5 = 675. Then 675 × 2 = 1350! Totally forgot to multiply by the 2 at the end. The actual LCM is 2 × 3 × 3 × 3 × 5 × 5 = 1350. Divided: 1350 ÷ 135 = 10, 1350 ÷ 150 = 9. Perfect fit. Lesson? Don’t rush the final multiply!
Why Bother?
Feels kinda pointless just factoring numbers? Maybe. But figuring out the shared tools (GCF) is like knowing the biggest measuring cup that fits both your flour and sugar containers. And the super number (LCM)? Imagine baking, needing whole batches – when do the weird recipe sizes like 135g and 150g sync up? Answer: every 1350 grams. Suddenly those prime bits feel useful, sitting right there in your kitchen cupboard.