So yesterday I got totally stuck on this algebra problem involving multiple factors, right? The number 135 kept popping up and I realized I couldn’t brute force my way through. Like, what is 135 made of? I vaguely remembered something about prime factors, so I figured why not dive back into it properly.
Dusting Off The Basics
First things first, I grabbed a pen and paper. I started simple: I know primes are numbers only divisible by 1 and themselves – 2, 3, 5, 7, 11, and so on. The goal was to break 135 down into a product of ONLY prime numbers.
The Trial and Error Phase
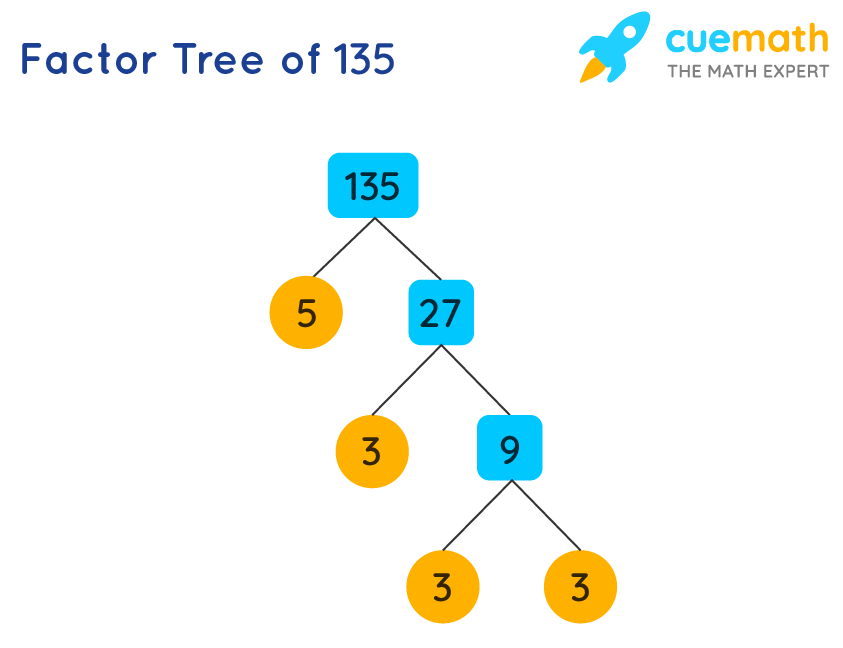
I looked at 135. It ends with a 5, so obviously it’s divisible by 5. Quick mental check: 135 ÷ 5 = 27. Okay, so one prime factor is 5, and now I have 27 to deal with.
27… that’s 3 cubed, right? 3 times 9? No, 3 x 9 is 27, but 9 isn’t prime. So I split that further: 27 ÷ 3 = 9. Now I have a 3. Then 9 ÷ 3 = 3. Now I have another 3. Then 3 ÷ 3 = 1. Done. So 27 breaks down to 3 x 3 x 3.
Putting It All Together
Let’s collect those pieces. We had:
- Divided 135 by 5 to get 27
- Divided 27 by 3 to get 9
- Divided 9 by 3 to get 3
- Divided 3 by 3 to get 1
That means the prime factors are: 5, 3, 3, 3.

So the prime factorization is 5 × 3 × 3 × 3. We usually write it neatly using exponents: 135 = 3³ × 5. Double-checked it: 3 cubed is 27, times 5 is 135. Perfect.
Why Bother Though? The Lightbulb Moment
Okay, cool, I found the prime factors. But how is this actually useful? That was the question. Here’s where it clicked during my practice:
- Simplifying Fractions: If you get a big ugly fraction like 270/405, spotting shared prime factors is a lifesaver. Both numbers share factors of 3 and 5? Makes simplifying waaay faster.
- Finding GCD/LCM: Greatest Common Divisor and Least Common Multiple suddenly become less scary. Just look at the prime factors! For GCD, take the smallest power of each shared prime. For LCM, take the highest power of all primes present. Boom.
- Spotting Divisors: Knowing the prime factors of 135 (3³ × 5) instantly tells me that only prime factors of 3 and 5 will divide evenly into it. Any number made from multiplying different combinations of 3s and 5s (like 1, 3, 9, 5, 15, 45, 27, 135) is a divisor. No guesswork.
- Patterns & Rules: Seeing that 135 has both a factor of 5 and a factor of 3 explains why it follows the divisibility rules for 5 (ends in 0 or 5) AND 3 (digits sum to 9, which is divisible by 3). The prime factorization reveals the underlying rules.
So yeah, taking those few minutes to figure out why 135 breaks down to 3³ × 5 wasn’t just about that one number. It gave me tools – faster ways to handle messy fractions, find what numbers have in common, list divisors, and understand why certain divisibility tricks work. Definitely worth the scratch paper!